Doing More Than One Operation

What if you want to write 3 + 4 * 5 in ClojureScript? A function box diagram of this expression looks like this:

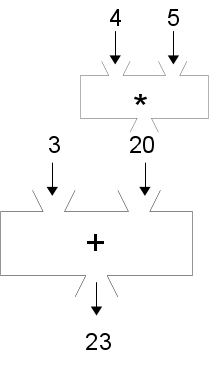
Box multiplying 4 * 5 -> 20, feeding into add box with 3 as other input

Two operations as function boxes

There are two ways to translate an arithmetic expression from its normal infix (operator between the operands) notation to ClojureScript’s prefix (operator before the operands) notation: the logical, abstract thinking method and the mechanical, no-thinking method.

Expressions: The Abstract Thinking Method

What’s Really Going On?

As you saw from the function box diagram, 3 + 4 * 5 means to add 3 to the result of multiplying 4 times 5. (That’s the order because multiplication is more important than division. This is referred to as precedence of operations.)

To add 3 to something in ClojureScript, you write:

(+ 3 something)

That something is the result of multiplying 4 times 5, which you write as (* 4 5). Putting it together, you get:

(+ 3 (* 4 5))

Notice that the order of operations is inverted—the last operation you do in infix notation (addition) becomes the first prefix operation.

Here’s another example: 3 - 2 * 4 / 5. Thinking it through in order of operations:

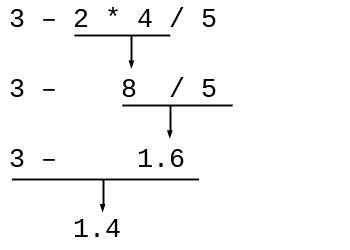
2 *4 -> 8, 8 / 5 -> 1.6; 3 - 1.6 -> 1.4

Order of evaluation for 3 - 2 * 4 / 5

Keeping in mind that the last shall be first, and the first shall be last, the answer is:

(- 3 (/ (* 2 4) 5))

Expressions: The Mechanical Method

Let’s return to the expression 3 + 4 * 5. Fully parenthesize the expression, which gives you (3 + (4 * 5)). Then switch the first operand and the operator within each set of parentheses.

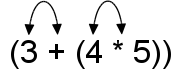
Arrows showing switch of 3 and +, 4 and *

Switching operator and operand

That gives you this result:

(+ 3 (* 4 5))

As before, the order of operations is inverted; the last operation you do in infix notation (the addition) becomes the first prefix operation.

Here is the other example: 3 - 2 * 4 / 5. Using what you know about order of operations and fully parenthesizing the expression, you apply these steps:

(3 - ((2 * 4) / 5))     ; fully parenthesize
(- 3 ((2 * 4) / 5))     ; switch 3 and minus sign
(- 3 ((* 2 4) / 5))     ; switch 2 and multiplication symbol
(- 3 (/ (* 2 4) 5))     ; switch (* 2 4) and division symbol

No, I have not pulled a fast one on you with that last step. I really am following the rule: I switched the operator (the division) with the first operand of the division, which, in this case, was (* 2 4).

Now it’s your turn to give it a try on the next page.

Next Section - Exercises in Arithmetic