Manipulating Collections - reduce

The map function creates a new sequence with the same number of items as in the original collection. Sometimes, however, you want to process a collection and get a single item as a result; for example, you might want the minimum or maximum of a list of numbers, their sum (in order to compute the average), or their sum of squares (to compute standard deviation). This is where the reduce function comes into play

The reduce function

reduce is also a higher-order function; it takes a function as one of its arguments and applies that function to each element of the collection to accumulate a result; that is, it “reduces” the collection to a smaller result (in most cases, a single piece of data).

Here is the general form of the reduce function that we will use:

(reduce f initial collection)

where

  • f is a function that has two parameters: the current accumulated result and the item under consideration
  • initial is the initial value of the accumulated result
  • collection is the collection to be reduced

As an example, here is reduce used to calculate the sum of squares of a set of numbers:

Here is the sequence of calls and results as reduce does its job:

  • reduce starts by using 0 (the initial value) and 2 (the first item in the collection) as inputs to sumsq. The output of (sumsq 0 2) is 4.
  • That becomes the new accumulated result; reduce will then call sumsq with 4 and 3 as its inputs. The output of (sumsq 4 3) is 13...
  • so 13 becomes the result as reduce calls sumsq with 13 and 5 as its inputs. The output of (sumsq 13 5) is 38.
  • As the collection has been entirely processed, 38 is returned as the value of the entire call to reduce.

Here’s a video that shows how it works:

If you do not provide an initial value, reduce will use the first two values in the collection as input to the reducing function. So, if you wanted to find the sum of all the values in a vector, you could simply do the following, which uses a longer vector for clarity:

This works because + is a function that takes two arguments. The sequence of calls and results as reduce proceeds is:

  • The first call to + is (+ 2 3) (the first and second items in the collection), resulting in 5.
  • The 5 becomes the first argument, and 7 the second argument, giving (+ 5 7), resulting in 12
  • The 12 becomes the first argument and 4 the second argument, giving (+ 12 4), resulting in 16
  • As there are no more items in the collection, the final result of reduce is 16.

Exercises

Exercise 1: Write a program that uses reduce to find the maximum value in a collection. You will want to use the no-initial-value version of reduce here; before you look at any other values, the initial value of the maximum should be the first item in the collection.

Exercise 2: Write a program that uses reduce as part of finding the average value of a collection of numbers. Remember that the count function tells you how many items are in a collection. If you are handed an empty collection, return 0 as the value for the average (a reasonable compromise rather than giving an error message).

Exercise 3: Write a program that uses reduce as part of finding the standard deviation of a collection of numbers. Here is the formula:

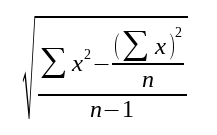
square root of ((sum of x**2 - ((sum of x)**2 / n) / (n - 1))

Formula for standard deviation

Σx2 is the sum of squares; (Σx)2 is the sum of the items, squared. Return zero if there are less than two items in the collection.

Next Section - Manipulating Collections - reduce (part 2)