Manipulating Collections - reduce (part 2)¶

Let’s return to the formula for standard deviation:

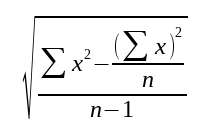
Formula for standard deviation

On the preceding page, the solution used reduce twice; once to find the sum, and again to find the sum of squares. Wouldn’t it be nice if you could get the sum and sum of squares with just one call to reduce? It would, and you can. There’s no law that says reduce has to reduce to a single number. It can produce a single vector with two elements—the sum and the sum of squares:

First, look at the call to reduce. It follows the established pattern: the arguments are a function sum-and-sumsq, an initial value for the result [0 0], and the collection to be reduced [1 3 5 2]. The only difference is that the initial value is now a vector, not a single number.

Now, look at the sum-and-sumsq function. As with the previous examples of reduce, it has two arguments: the accumulated result and an item from the collection. The result of the function is a new vector that adds the value to the first item in the result and the value squared to the second (last) item in the result.

Given this, here is an updated version of the standard deviation calculation:

Remember back in the preface, where you saw the graph of this vector of high and low temperature sub-vectors (now bound to a symbol):

(def temperatures [[3 9] [2 13] [4 10] [4 9] [4 12] [9 20] [16 21]])

To create the graph, you will need to split the vector into two vectors: one of high temperatures and one of low temperatures:

[[3 2 4 4 4 9 16]
[9 13 10 9 12 20 21]]

Now that you know that reduce can yield a result of any sort, you can write a function that reduce will use to split up the tempetature vector. The result is going to be a vector of two vectors, so the initial result is [[][]], and the call will be:

(reduce split-temperatures [[][]] temperatures)

Before just starting to write code, again, let’s analyze what needs to happen here. I was trying to describe this in words, and was getting nowhere, until I drew a diagram that shows what happens when the function processes the first two sub-vectors in the temperatures vector:

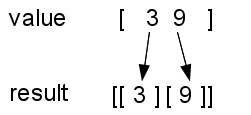
In the preceding image, the first entry in the value (3) is added to the first result vector, and the second entry in the value (9) is added to the second result vector.

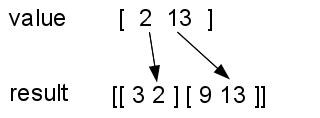
And, when processing the second item, the first entry in the value (2) is added to the first result vector, and the second entry in the value (13) is added to the second result vector.

Given this information, write the split-temperatures function. Hint: use conj to add elements to a vector.