Functions¶

The heart of functional programming is, of course, the function. Here’s a brief review of what a function is.

Functions as “Black Boxes”¶

You can think of a function as a “black box” that takes some input or inputs and provides some output. Here’s a picture of a black box that adds whatever two numbers come into its input hopper:

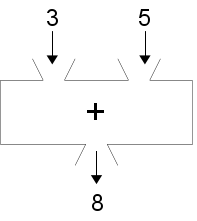
Addition as a function box

If you were to write this in a pseudo-mathematical notation, you could write something like this:

add(3, 5) → 8

Here’s another black box that finds the average of its inputs:

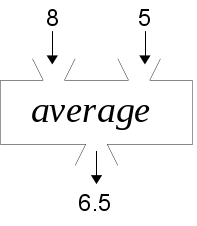
Box with 8 and 5 as input, 6.5 as output

Averaging as a function box

In mathematics-like notation, average(8, 5) → 6.5

Functions in Functions¶

If you were to take an X-ray of the average box, you would find that it contains two function boxes inside it:

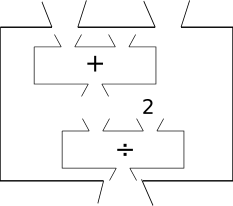
Box with an add and divide by 2 box in it

Inside the averaging box

In our pseudo-mathematical notation, using generic variable names instead of 8 and 5, you could write this: average(a, b) ⇒ divide(add(a, b), 2).

Before leaving this subject, it’s worth noting that the add, divide and average functions are all pure functions; if you give them the same input, you will always, always get the same output. Keeping your functions as pure as possible is a Good Thing™. Yes, there are non-pure functions, and you will see them in upcoming chapters.