The idea for this article came to me while I was writing a program in an entirely different language. I had a spreadsheet with days of the week as columns and hours of the day as its rows, and I needed it with the hours as the columns and the days as rows. In math, a spreadsheet is called a matrix, and switching rows and columns is called transposing the matrix. After finishing the spreadsheet program, I wondered how I would approach the problem of transposing a matrix in Elixir.

The Problem at Hand

Given a matrix represented as a list of lists:

[[1, 2, 3, 4],
 [5, 6, 7, 8],
 [9,10,11,12]]

write a function that will transpose the matrix (that is, switch rows and columns). I’ve formatted the numbers so you can see what I mean more clearly.

[[1, 5, 9],
 [2, 6, 10],
 [3, 7, 11],
 [4, 8, 12]]

Now, if this were your typical imperative language like C/C++, Java, you name it, you’d just write some nested for loops and the problem would be solved.

In Elixir, though, you are encouraged to think in terms of functions and recursion rather than iterative loops. The key to working with lists in a recursive way is to write your functions like this:

  • Divide the list into its first item (the head) and the remaining items (the tail).

  • Process the head of the list.

  • Now look at the remaining items.

    • If there are no remaining items, your job here is done.

    • If there are remaining items, well, they’re a list, too, just like the original list, only smaller. Simply call this function and pass it the tail of the list. (There’s your recursion.)

Here’s how this applies to the problem of transposing a matrix. Call a function and pass it the matrix as its first argument. The second argument to this function will be the “result so far,” which is an empty list at the beginning. The first thing the function does is to separate the head (the first row of the matrix) from the tail.

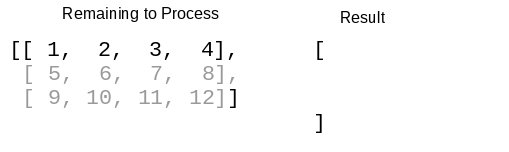
Starting configuration

Process the head by flipping it on its side and attaching it to the result matrix. (For the moment, don’t worry about how this happens. We’ll get to it soon.)

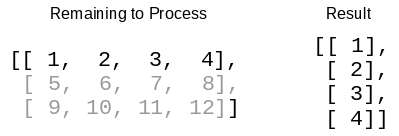
First row attached as a column

Now that the head of the matrix is taken care of, call the function again and give it the tail of the matrix as the first argument and the result so far as the second argument:

Remaining rows of matrix highlighted

The function once again has a matrix; just a slightly smaller one. It separates the head and tail of this matrix, and once again flips the head on its side and attaches it to the result.

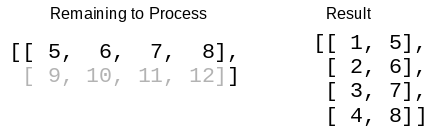
Head of remainder highlighted

…and then calls the function yet again with the remaining row and the new result as the arguments.

At some point, you won’t have any remaining rows, so whatever is in the result will be your transposed matrix.

This worked out to the following Elixir code. Since I haven’t addressed the problem of flipping a row on its side, the make_column/2 function is just a placeholder that adds the row, unchanged, to the start of the result.

defmodule Transpose1 do
  def transpose(m) do
    attach_row(m, [])
  end

  def attach_row([], result) do  # handle ending case first
    result
  end

  def attach_row(row_list, result) do
    [first_row | other_rows] = row_list
    new_result = make_column(first_row, result)
    attach_row(other_rows, new_result)
  end

  def make_column(row, result) do
    [row | result]
  end
end

If you put this code in a file named transpose1.ex, compile it, and call the function, you’ll get this result:

iex(1)> c("transpose1.ex")
[Transpose1]
iex(2)> Transpose1.transpose([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
['\t\n\v\f',[5,6,7,8],[1,2,3,4]]
Note (The '\t\n\v\f\' is really the list [9,10,11,12]; iex displays it as a character list.)

Notice that the rows are in the reverse order because I put them in at the beginning of the result list. This happens a lot when you construct lists in Elixir.

The next question is how to flip a row on its side to make it into a column. You can handle this recursively as a function that takes a row as its first argument and the “result so far” as its second argument.

  • Divide the row into its first item (head) and remaining items (tail).

  • Divide the result into its first result row (head) and remaining result rows (tail).

  • Put the first item into the first row of the result.

First item of row is added to first row in results

  • That new first row is followed by the result of calling the function recursively with the remaining items and remaining result rows.

First of remaining items is added to first row in remaining results

When you run out of remaining items in the row you’re trying to flip on its side, you have finished the task.

Here is what the three clauses of the new make_column/2 function do:

  • When there are no more entries in the row, the column you are making is complete.

  • Make the row into a column when the result matrix is empty. Create the first item as a singleton list. Follow it with the result of making the remaining entries in the column.

  • Make a row into a column when the result matrix is not empty. Do this by adding the first item at the beginning of the first row of the result. That list is followed by the result of making the remaining entries in the column 

  def make_column([], result) do # my job here is done
    result
  end

  def make_column(row, []) do
    [first_item | other_items] = row
    [[first_item] | make_column(other_items, [])]
  end

  def make_column(row, result) do
    [first_item | other_items] = row
    [first_row | other_rows] = result
    [[first_item | first_row] | make_column(other_items, other_rows)]
  end

Here’s what happens when you compile and run this new code:

iex(1)> c("transpose1.ex")
/home/examples/article2/transpose1.ex:1: redefining module Transpose1
[Transpose1]
iex(2)> Transpose1.transpose([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
[[9,5,1],[10,6,2],[11,7,3],[12,8,4]]

Oops. When flipping a row, new items are added at the beginning of the result rows, so each row of the transposed matrix is in the wrong order. No problem; just write yet another recursive function to reverse each of the rows once all the input rows are processed.

The first clause of reverse_rows/2 prepends the reversed row to the reversed matrix.

The first clause finishes the recursion. Because I’m adding the reversed rows in reverse order (!!), I have to do one final Enum.reverse to set matters right when the job is done.

See if you can figure out how the reverse_rows/2 function’s recursion follows the pattern that I established at the beginning of this article.

  def attach_row([], result) do
    reverse_rows(result, [])
  end

  def reverse_rows([], result) do
    Enum.reverse(result)
  end

  def reverse_rows(rows, result) do
    [first | others] = rows
    reverse_rows(others, [Enum.reverse(first) | result])
  end

And voilà, it works:

iex(3)> c("transpose1.ex")
/home/examples/article2/transpose1.ex:1: redefining module Transpose1
[Transpose1]
iex(4)> Transpose1.transpose([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
[[1,5,9],[2,6,10],[3,7,11],[4,8,12]]

Here’s the entire Elixir file.

Tail Recursion and Moral Purity

This code works, and it’s perfectly acceptable. If you look at the recursion in attach_row/2 and reverse_rows/2, you will see that the recursion is the very last thing in the function. When you write a function in this way, it is called tail recursive, and Elixir can optimize it so that it runs quickly.

The make_column function is recursive, but it’s not tail recursive. Look at its last line:

[[first_item | first_row] | make_column(other_items, other_rows)]

The recursive call creates the remainder of the column, and then that result is appended to the list. That means that the recursive call isn’t the very last thing to happen in the function, and it’s possible that Elixir won’t be able to optimize the code. If I had an extremely large matrix with hundreds of thousands of rows, the program might use large amounts of memory or take longer. (But of course, I’d measure where the memory usage or slowdown really was before changing the code!)

If you aren’t dealing with huge amounts of data (for example, in the schedule program I was talking about at the start of this article, the matrix had only 7 columns and 60 rows), it’s perfectly acceptable to have a non-tail-recursive call.

However, many programmers consider it to be more “morally pure” to make all function calls tail recursive. In order to convert make_column/2 into a tail recursive function, I had to add an extra argument that keeps track of the current state of the result and accumulates the new information, passing that on to the next function call. This extra argument is thus also referred to as an accumulator. You’ll see accumulators used quite often in tail-recursive code.

Here’s what the new version, make_column/3 looks like graphically:

Call the function with a row, the current transposed matrix, and the accumulator for the next stage. (The accumulator starts out empty.)

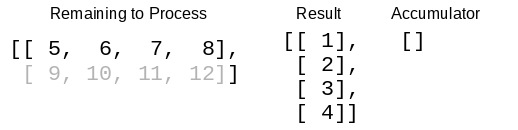
shows three lists

Take the head of the row and the head of the current transposed matrix, and put that row into the accumulator.

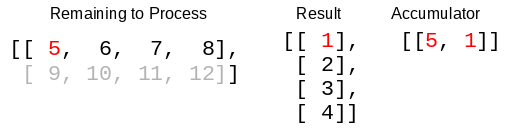
Shows [5

Now make a recursive call, passing the remaining items in the row, the remaining rows of the result, and the accumulator.

Shows shorter lists and accumulator

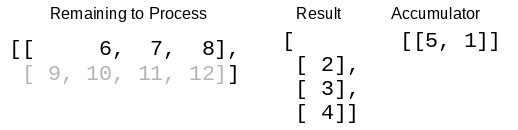
The function once again takes the head of the row and the head of the transposed matrix, and puts that row into the accumulator.

Shows second row added to the accumulator

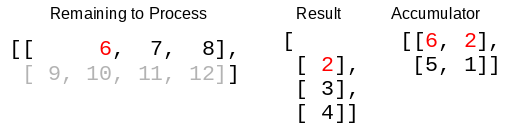
This continues on until there are no more items left in the row, at which point the accumulator will contain the new transposed matrix (in reverse order of rows).

Note In the preceding diagrams, I’m showing the items being added at the beginning of the list, exactly as the Elixir code does it.

Here’s the revised code. The second clause is used when the transposed matrix is empty (for the first row of the original matrix).

  def make_column([], _, new) do
   Enum.reverse(new)
  end

  def make_column(row, [], accumulator) do
    [row_head | row_tail] = row
    make_column(row_tail, [], [[row_head] | accumulator])
  end

  def make_column(row, result, accumulator) do
    [row_head | row_tail] = row
    [result_head | result_tail] = result
    make_column(row_tail, result_tail, [[row_head | result_head] | accumulator])
  end

There’s a little bit more code here, but it is now tail recursive and morally pure, and it still works.

iex(5)> c("transpose2.ex")
[Transpose2]
iex(6)> Transpose2.transpose([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
[[1,5,9],[2,6,10],[3,7,11],[4,8,12]]

Here’s the entire Elixir file.

Conclusion

Remember the generic pattern for a function that works with lists recursively:

  • Divide the list into its first item (the head) and the remaining items (the tail).

  • Process the head of the list.

  • If no items remain, you have finished; otherwise, call the function and pass it the tail of the list.

Learn to love recursion; it’s one of the most powerful tools available to you in Elixir and other functional programming languages.